Geant4 geometry translation¶
A logical volume can be referenced multiple times, i.e., placed multiple times in multiple different volumes. The Geant4-ORANGE converter decomposes the graph of logical volume relationships into subgraphs that each become a CSG unit. This decomposition is currently tuned so that:
Volumes with no children are directly placed as “material” leaf nodes into a unit
Logical volumes placed in a singular location without transforms are also placed as materials with child volumes explicitly subtracted out
Union or poly volumes (for now!) must be placed as materials even if they are used multiple times and have daughter volumes.
Volume mapping¶
Accurately determining the unique instance associated with a particle track’s location—analogous to the touchable history in Geant4— requires establishing a bijective mapping between each ORANGE implementation volume and its corresponding volume or volume instance in the canonical volume hierarchy.
The construction and execution phases proceed as follows:
Conversion to unit protos: During the translation of local and physical volumes into unit protos and volume definitions (material placements, background, and daughters), each child volume placed within an already-instantiated parent is marked as residing inside a parent material. This step records a new local parent entry in the unit proto input, establishing logical connectivity even when volumes are side-by-side in the implementation. Because canonical volume IDs are not yet assigned at this stage, the proto input stores the proto material ID instead—that is, the identifier of the parent volume placement after subtracting its children.
Proto build and ID remapping: When building the proto, the stored local material identifiers are remapped to canonical volume IDs. The resulting associations are recorded in the unit input as a local parent map.
Geometry flattening: During geometry flattening by the UnitInserter, two vectors are generated for each universe: (1) a local parent volume vector, giving the implementation volume ID of the canonical parent volume for each entry; and (2) a local volume level vector, specifying the level of each volume relative to its enclosing universe, to handle inlined universes.
Execution and traversal: At runtime, the total volume level for a given track is computed by summing the local volume levels across all universes in the stack. The complete volume hierarchy for the current instance is then reconstructed by recursively traversing backward through the local parent links.
Consider a geometry with volumes World, A–D, X, and Y. Some of these volumes have multiple placements, and one instance of X also has a rotation. Figure 1 illustrates the overall geometry layout.
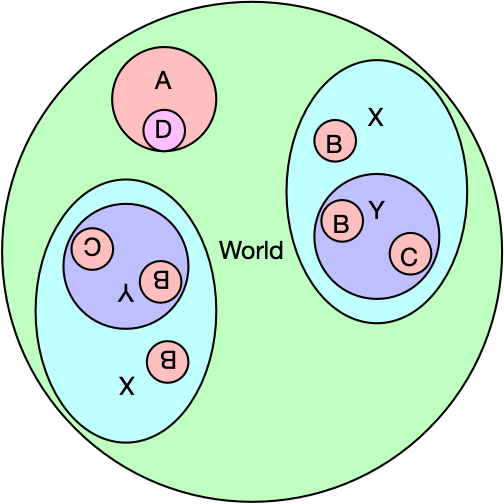
Fig. 1 Example geometry containing repeated and rotated volumes.¶
This geometry produces the volume hierarchy shown in Figure 2. Although there are four canonical volume levels, ORANGE converts the hierarchy into three universes (U, V, and W). Leaf volumes (i.e., those with no children) are inlined into the same universe as their parent, and single-use enclosures such as D are usually inlined as well.
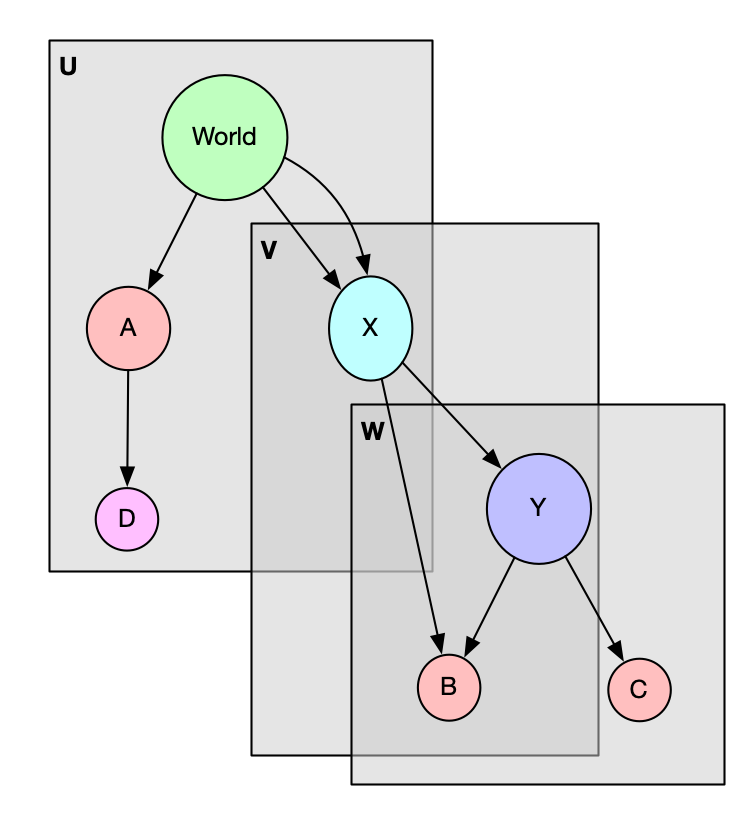
Fig. 2 Volume hierarchy and corresponding ORANGE universes. Arrows indicate “local volume parent” relationships, and “local volume level” numbers are shown on the left.¶
Each ORANGE universe contains a small set of local implementation volumes. From an implementation perspective, these are all equal regardless of whether the canonical volume it represents is at a higher or lower level. Most of these local volumes are volume instances: specific transformed placements in the geometry. However, the outermost enclosing volume (either a “background” volume” or an volume with daughters subtracted out) corresponds to a true volume, since it can be instantiated multiple times as a child of an enclosing universe. Figure 3 shows these relationships.
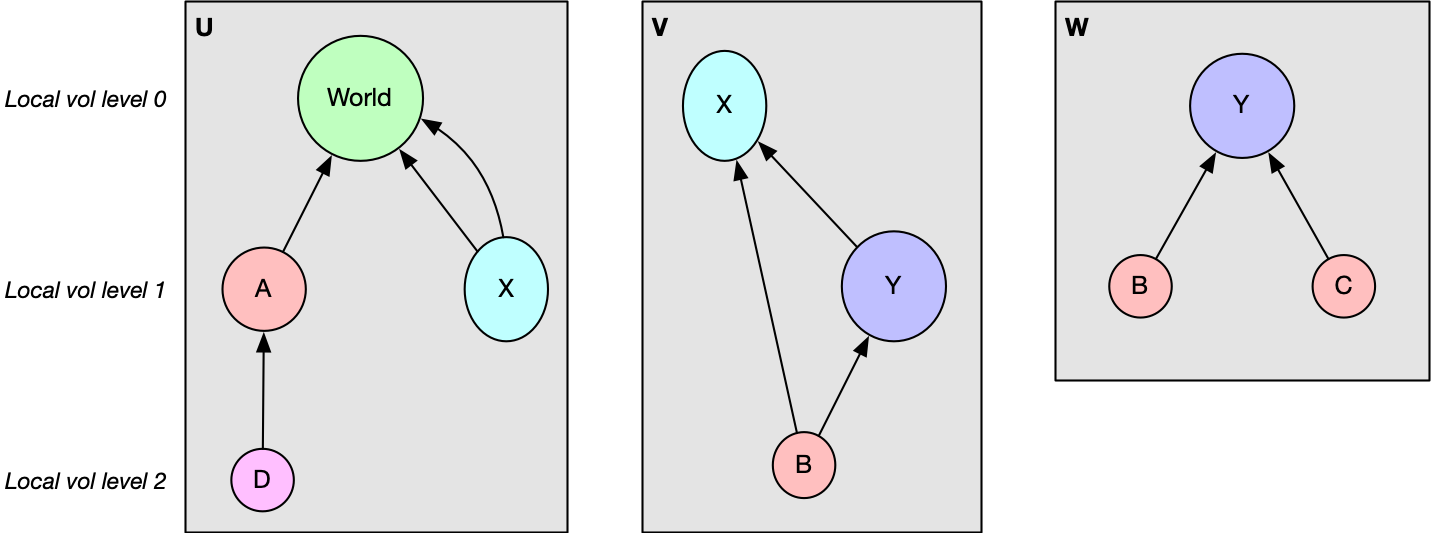
Fig. 3 Local impl volumes in each universe. Top nodes are true volumes; lower nodes represent inlined instances.¶
An ORANGE state consists of a stack of pairs [{universe, impl volume}, ...].
When using volume instances rather than volumes, this stack defines the unique
placement in the full geometry. Table 7
provides an example of the correspondence between the volume path, ORANGE
state, and computed local levels in this example geometry.
Volume path |
Volume level |
ORANGE state |
Local levels |
|---|---|---|---|
World→X→Y→C |
3 |
{U, X}, {V, Y}, {W, C} |
{1, 1, 1} |
World |
0 |
{U, World} |
{0} |
World→A→D |
2 |
{U, D} |
{2} |
World→X→B |
2 |
{U, X}, {V, B} |
{1, 1} |
World→X |
1 |
{U, X} |
{1} |
Configuration¶
For debugging purposes, a special struct can be deserialized from a JSON input
file specified with the G4ORG_OPTIONS environment variable.
-
enum class celeritas::inp::InlineSingletons¶
How to inline volumes used only once.
Values:
-
enumerator none¶
Never.
-
enumerator untransformed¶
Only if not translated nor rotated.
-
enumerator unrotated¶
Only if translated.
-
enumerator all¶
Always.
-
enumerator size_¶
-
enumerator none¶
-
struct OrangeGeoFromGeant
Construction options for Geant4 conversion.
Note that most of these should never be touched when running an actual problem. If the length unit is changed, the resulting geometry is inconsistent with Geant4’s scale.
Warning
Currently ORANGE tracking requires:
inline unions to be true (see https://github.com/celeritas-project/celeritas/issues/1260)
remove_interior to be true (see https://github.com/celeritas-project/celeritas/issues/2012 )
Problem scale and tolerance
-
double unit_length = {celeritas::lengthunits::millimeter}
Scale factor (input unit length), customizable for unit testing.
-
Tolerance tol
Construction and tracking tolerance (native units)
Structural conversion
-
unsigned int explicit_interior_threshold = {2}
Volumes with up to this many children construct an explicit interior.
-
bool inline_childless = {true}
Forcibly inline volumes that have no children.
-
InlineSingletons inline_singletons = {InlineSingletons::untransformed}
Forcibly inline volumes that are only used once.
-
bool inline_unions = {true}
Forcibly copy child volumes that have union boundaries.
-
bool remove_interior = {true}
Replace ‘interior’ unit boundaries with ‘true’ and simplify.
-
bool remove_negated_join = {false}
Use DeMorgan’s law to replace “not all of” with “any of not”.
Debug output
-
bool verbose_volumes = {false}
Write output about volumes being converted.
-
bool verbose_structure = {false}
Write output about proto-universes being constructed.
-
std::string objects_output_file
Write converted Geant4 object structure to a JSON file.
-
std::string csg_output_file
Write constructed CSG surfaces and tree to a JSON file.
-
std::string org_output_file
Write final org.json to a JSON file.